فصل پنجم ریاضی نهم یکی از مهمترین فصول کتاب درسی ریاضی نهم است که هر سال سوالاتم مهمی از آن در امتحان نهایی میآید. همچنین این فصل مقدمهای برای فصل هفتم نیز هست و سالهای آینده از مباحث این درس بسیار استفاده خواهد شد. پس این فصل را جدی بگیرید و با دقت آموزشها را پیگیری کنید. یادتان باشد ریاضی را با نوشتن یاد میگیرید پس قلم و کاغذ جلوی دستتان باشد و بنویسید.
درس اول: عبارتهای جبری و مفهوم اتحاد
یادآوری
سال گذشته در فصل چهایرم ریاضی هشتم با مطالب متنوعی از عبارتهای جبری آشنا شدید. در ویدیو اغازین این فصل مطالب مهمی که باید از سالهای گذشته به یاد داشته باشید را با هم مرور میکنیم. از جمله به تعریف دقیق تک جملهای و چندجملهای ها میپردازیم.
درجه چندجملهای
منظور از درجه چندجملهای همان توانهای متغیرهاست. در این ویدیو ابتدا با درجه یک جملهای ها نسبت به یک یا چند متغیر آشنا میشوید. سپس با درجه چندجملهای آشنا میشوید. در آخر هم چندجملهای استاندارد را معرفی میکنیم و به بهتان یاد میدهیم چگونه یک چندجملهای را به ترتیب درجههایش مرتب کنید.
تعریف اتحاد و تفاوت آن با معادله
اتحاد یک مفهوم جدید است که امسال در فصل ۵ ریاضی ۹ برای اولین بار با آن آشنا میشوید. در ویدیو توضیح می دهیم که یک تساوی جبری چه زمانی اتحاد است و چه زمانی معادله است و چگونه تفاوت آنها را تشخیص دهیم. امسال با ۴ اتحاد مهم آشنا میشوید و از این پس هر سال با اتحادهای جدیدی رو به رو خواهید شد.
اتحاد مربع دوجملهای

اولین اتحاد مهم و معروف تریت اتحادی که با آن آشنا میشوید اتحاد مربع دوجملهای است. در این ویدیو ابنتدا فرمول اتحاد مربع بیان میشود سپس معادل کلامی و هندسی آن را شرح میدهیم و با کمک آن مثالهای متوعی حل میکنیم.
تجزیه عبارتهای جبری با فاکتورگیری
شما سال گذشته با تجزیه عبارتهای جبری آشنا شدید. منظور از تجزیه یک عبارت جبری نوشتن آن به صورت حاصل ضرب دو عبارت جبری سادهتر است. در فصل ۴ ریاضی ۸ با روش فاکتورگیری آشنا شدید. در این ویدیو روش فاکتورگیری را خیلی سریع مرور میکنیم و مثالهای پیشرفتهای با آن حل میکنیم.
تجزیه با اتحاد مربع دو جملهای
گاهی اوقات یک عبارت جبری را نمیتوان با روش فاکتورگیری تجزیه کرد. در این صورت اتحادها میتوانند راهگشا باشند. در این ویدیو توضیح میدهیم چه زمانیس میتوان برای تجزیه عبارت جبری از اتحاد مربع دوجملهای کمک گرفت. همچنین روش این تجزیه را نیز با مثالهای متعدد توضیح میدهیم.
درس دوم: چند اتحاد دیگر، تجزیه و کاربردها
اتحاد مربع سه جملهای
پس از آن که با اتحاد مربع دوجملهای آشنا شدیم، نوبت به اتحاد مربع سه جملهای رسیده است. در این ویدیو کوتاه فرمول اتحاد مربع سه جملهای همراه با مثالهای گونانگون بیان شده است.
اتحاد مزدوج
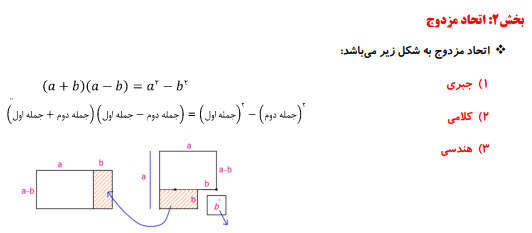
یکی از اتحادهای پرکاربرد در ریاضی اتحاد مزدوج است. در این ودیو صورت های مختلف اتحاد مزدوج را میبینید. سپس با مثالهای متعدد کاربرد آن در ساده کردن را مشاهده میکنید. با اتحاد مزدوج هم می توان مسئلههای پیچیدهای طراحی کرد که نمونههایی از آن را در ویدیو مشاهده خواهید کرد.
تجزیه با اتحاد مزدوج
چه زمانی میتوان یک عبارت را با اتحاد مزدوج تجزیه کرد؟ چگونه این کار را انجام دهیم؟ سوالاتی است که در این ویدیو با مثالهای متنوع و امتحانی به ان ها پاسخ داده میشود.
اتحاد جمله مشترک

اتحاد مهم دیگر که در فصل پنجم ریاضی نهم به آن پرداخته میشود اتحاد جمله مشترک است. در این اتحاد دو پرانتز در هم ضرب میشوند که یک بخش مشترک و یک بخش غیرمشترک دارند. در این ویدیو اتحاد جمله مشترک را کامل تشریح میکنیم و مثالهای متعددی از آن حل خواهیم کرد.
تجزیه با اتحاد جمله مشترک
اگر فرمول اتحاد جمله مشترک را به خوبی درک کرده باشید، حال میتوانید تجزیه آن را به سادگی یاد بگیرید. در این ویدیو می آموزید چه موقع و چگونه یک عبارت جبری را با اتحاد جمله مشترک تجزیه کنید.
نکات تکمیلی اتحاد
اتحاد مکعب دوجملهای
اتحاد مکعب دوجملهای در فصل ۵ ریاضی ۹ نیامده است ولی برای دانشآموزان تلاشگر دانستن این اتحاد جذاب است. از طرفی سال دهم که با آن آشنا شوید کارتان راحت تر میشود. در اتحاد مکعب دوجملهای روی پرانتز توان سه داریم. در ویدیو کوتاه زیر فرمول و مثالها توضیح داده شده است.
اتحادهای دوجملهای (بسط نیوتن) و مثلث خیام پاسکال
با دیدن فرمول اتحاد مربع و مکعهب دوجملهای این سوال به ذهن میرسد که برای توانهای بیشتر چه کنیم؟ در ویدیو پیش رو توضیح میدهیم که اگر توانهای بزرگتری در اتحاد دوجملهای وجود داشت، چگونه آنها را ساده کنیم. برای محاسبه ضرایب از مثلث خیام پاسکال استفاده کردهایم.
نابرابریها و نامعادلهها
نابرابری(نامساوی)
در این بخش از فصل پنج ریاضی نه توضیح میدهیم منظورمان از نابرابری یا نامساوی چیست و چه شکلهای متفاوتی دارد. همچنین نمایش هندسی نابرابریها روی محور را نشان میدهیم. همچنین به شما آموزش میدهیم چگونه با یک تساوی یک نامساوی تشکیل دهید و دو متغیر را با هم مقایسه کنید. این ویدیو مقدماتی به شما برای درک بهتر نامعادلهها کمک میکند.
تعیین علامت عبارتهای جبری
یکی از سوالات پرتکرار فصل پنجم ریاضی نهم تعیین علامت عبارتهای جبری است. البته این موضوع به دو شکل مطرح میشود. ارتباط این بحث به نامساوی این است که علامت مثبت و منفی را با بزرگتر یا کوچکتر از صفر نشان میدهیم.
خواص نامساویها و تعریف نامعادله
همانطور که تساویها دارای خواص خاصی هستند، نامساویها هم دارای ویژگیهایی هستند. در این ویدیو این خاصیتها را توضیح میدهیم که بعدا برای حل نامعادله به کمک ما میآیند. در ادامه تعریف دقیق نامعادله را بیان میکنیم و منظور از مجموعه جواب نامعادله را روشن میسازیم.
روش حل نامعادله
روش حل نامعادله بسیار ساده است. میتوان گفت روش حل نامعادله با معادله تفاوتی ندارد، تنها در یک مرحله، زمانی که ضریب مجهول منفی شود تفاوتی ایجاد میشود. در ویدیو زیر انواع حالتهای نامعادله از ساده تا پیشرفته بیان شدهاست.
کلام آخر
امیدواریم مطالب این فصل را به خوبی فرا گرفته باشید. در انتهای صفحه نظراتتان را با ما به اشتراک بگذارید. اگر باز هم در این فصل یا فصلهای دیگر ریاضی نهم مشکلی دارید و نیاز به کلاس خصوصی دارید میتوانید از لینک زیر درخواست خودتان را ثبت کنید. تمرین و حل سوالات بیشتر را فراموش نکنید. موفق باشید.
برای مشاهده سایر تدریسهای ریاضی نهم به لینک زیر مراجعه کتید.

عالی مثل همیشه
خیلی عالی
استاد تو تکی
ممنون استاد .. من دهم تجربی ام امسال میرم یازدهم .. توی نهمم چون مجازی بودیم نتونستم نهم رو خوب جمع بندی کنم و حسابی تو دهم مشکل داشتم … ..
ممنون استادددد باتوضیح هات شما عاشق ریاضی شدممممم واقعا واقعاااا😂😂
تازه دارم ب این پی میبرم ک سال نهم واقعا تو تباهییی بودمم🤨😂ک درس نمیخوندم😂😂
خدارو شکر که برات مفید بوده
موفق باشی
واقعا عالیع.
من هر کاری میکنم یاد نم
عالی